自然数 の 総和
マレ ヴィラージュ 梶ヶ谷自然数の総和がゼータ関数の-1/12であることの新しい証明. 自然数の総和がゼータ関数の-1/12であることの新しい証明. K. Sugiyama[1] ゼータ関数の自然数和Z(-1)=1+2+3+…は発散する。. 一方、ゼータ関数の解析接続ζ(-1)="1+2+3+…". は-1/12に収束することが知られている。. 自然数の和はどのようにして-1/12に近づいてゆくの . 【まとめ】自然数の和の公式の求め方 ※いろいろな方法をご . ここでは といった自然数の和を扱います。. ここで紹介する1からnまでの和の公式は、以下のようになります。. 【1からnまでの和の公式】 begin {align*} & 1 + 2 + 3 + cdots + n = &a. 自然数の総和(無限和)1+2+3+4+…が-1/12になる事の視覚化 . 数と図形の分析. 2022.01.05 2024.02.27. 直感的には、自然数の総和1+2+3+4+…は無限∞である。 しかし、数学では、自然数の総和1+2+3+4+…は-1/12になるらしい。 正確には、"1+2+3+4+…"=-1/12であるらしいが、自然数を無限に足していくと、ある負の数が登場するのは奇妙に感じる。 そもそも、その負はどこから出てきたのかと疑問に思う。 そこで、俺は ∑∞ k=1kexp(−kx)cos(kx) ∑ k = 1 ∞ k e x p ( − k x) c o s ( k x) を使用して、自然数の総和が無限と-1/12になることを同時に直感的に視覚化した。 俺は無限級数1+2+3+4+…を次のように解釈した。. 自然数和は-1/12 | 日々の日記 - 理系ノート. 普通に計算したら無限大であるはずの自然数の総和が解析接続すると発散しないという面白い等式です。. zeta (-1)=1+2+3+cdots+ =-displaystylefrac {1} {12} ζ (−1) = 1 +2 + 3 +⋯+ = −121. zeta (s) ζ (s) はゼータ関数で、 zeta (s)=displaystylesum_ {n=1}^ {infty} displaystyle . モンスターズ インク の ツム
店 の 中【基本】和の公式(1からnまでの和) - なかけんの数学ノート. ここでは、1から n までの自然数の和について見ていきます。とてもよく出てくる公式が登場します。自然数の和一般項が $a_n=n$ となる数列 $ {a_n }$ を考えてみましょう。これは、 $1$ から順番に数字が並. 1+2+3+4+… - Wikipedia. 自然数 すべての総和 1 + 2 + 3 + 4 + … は、その n -次の 部分和. が 三角数 によって与えられる 無限級数 。 これは n を 無限大 に飛ばすとき際限なく増加するため、この級数は(正の無限大に) 発散 し、通常の意味での「和」を持たない。 (つまり、特別な意味では「和」を持つ。 一見するとこの級数が意味のある値を持つことは全くないように思われるが、これに数学的に意味のある値を結びつける方法があり、そうして得られた値は 複素解析 や、物理学における 場の量子論 、特に 弦理論 などの分野において応用がある。. 自然数やフィボナッチの総和がマイナス? 数学のトリックに騙さ . 自然数の総和. まず自然数の総和をSと置きましょう。 次に4Sを考え、以下のように計算します。 次に、-3Sをひとつずらしたものをこの式に足します。 ここで、1とマイナス1が交互に出る式が出てきました。 さらに、-6Sをずらして足し算しましょう。 ということで、 自然数の総和がマイナス12分の1 になってしまいました。 これを堂々とあっているかのような解説をしている人がいますが、これは 誤り です。 ではどこが間違っていたのでしょうか。 答えはひとつずらしたものを足すという行為です。 つまり、ひとつずらしたSはもとのSとは異なってしまうのです。 このように上の-3Sと3Sは異なります。 無限に足し合わせるものでも、ひとつずらしたものを等しいものとして計算することは間違っています 。. 1からnまでの和を求める公式 - 具体例で学ぶ数学. 図形を使った説明. 具体例. ・1 1 から 10 10 までの和. 1 + 2 + 3 + ⋯ + 9 + 10 = 1 2 × 10 × 11 = 55 1 + 2 + 3 + ⋯ + 9 + 10 = 1 2 × 10 × 11 = 55. ・1 1 から 100 100 までの和. 1 + 2 + 3 + ⋯ + 99 + 100 = 1 2 × 100 × 101 = 5050 1 + 2 + 3 + ⋯ + 99 + 100 = 1 2 × 100 × 101 = 5050. ・1 1 から 1000 1000 までの和. なぜゼータ関数の自然数の和は無限大に発散しないのか?. すると自然数 m が無限大となる条件で、オイラーマクローリンの総和公式は次のように表現できます。 ( オイラー=マクローリンの総和公式 ) ( 5 . 41 ). PDF ラマヌジャン と 自然数の総和. ラマヌジャン総和法は、級数の部分和に対するオイラー=マクローリンの公式の定数項だけを分離する方法である。 函数 f に対して、級数. の古典ラマヌジャン和 (classical Ramanujan sum) は. で定義される。 ここで f. (2k−1) は f の (2k − 1)-階導函数で B2k は 2k-番目のベルヌーイ数である (B2 = 1/6, B4 = −1/30 .) f(x) = x とすれば f の一階導函数が f (1) = 1 で残りはすべて消えるから、 は、 に置き換え正規化. リーマンゼータ. ζ(s) のグラフ. s > 1 で級数は収斂し. ζ(s) > 1 であることがわかる. 極 s = 1. の周りでの解析接続によって負の領域まで延長すれば. 自然数の正の約数の個数、総和、n乗の総和を求める公式 | 数学 . 自然数の正の約数の個数、総和、n乗の総和を求める公式 | 数学の庭. 整数. ある自然数 m が. m = p a ⋅ q b ⋅ r c ⋯. と素因数分解できるとき. m の正の約数の個数. ( 1 + a) ( 1 + b) ( 1 + c) ⋯. m の正の約数の総和. ( 1 + p + p 2 + ⋯ + p a) ( 1 + q + ⋯ + q b) ( 1 + r + ⋯ + r c) ⋯. m の正の約数の n 乗の総和. ( 1 + p n + p 2 n + ⋯ + p a n) ( 1 + q n + ⋯ + q b n) ( 1 + r n + ⋯ + r c n) ⋯. 例題. (1) 72 の正の約数の個数を求めよ。 (2) 72 の正の約数の総和を求めよ。. 自然数の1乗和・2乗和・3乗和の公式|4乗和・5乗和も紹介 | 合格 . 等差数列の和の公式 と 等比数列の和の公式 は簡単に求められる 数列 の和としてよく知られています.. この他に和がよく知られているものとしては. 梵天 の 湯 花火
捻挫 した 時 の 対処 法1乗和 1 + 2 + 3 + ⋯ + n. 2乗和 1 2 + 2 2 + 3 2 + ⋯ + n 2. 3乗和 1 3 + 2 3 + 3 3 + ⋯ + n 3. があります.この記事では. 1乗和・2乗和・3乗和の公式の証明. 4乗和・5乗和・……の公式の求め方. を順に説明します.. 「数列」の一連の記事. 数列の基礎. 1 最初の一歩は等差数列と等比数列! 2 等差数列の和の公式を直感的に理解する方法. 3 等比数列の和の公式を具体例から理解する. 4 数列の和を表せるシグマ記号Σの定義と性質. ある自然数の約数の総和を求める方法と考え方 | 高校数学の知識庫. 約数の総和とその求め方. ある自然数の約数を求めた後、その和を考えることにします。. 「なんで?. 」というツッコミは無しでお願いします(笑)。. 理由は"高校数学の整数の分野では結構問題に出てくるので覚えておくと便利だから"という . 【標準】和の公式(べき乗和の公式) - なかけんの数学ノート. 数列の分野で出てくる、自然数のべき乗和の公式を復習しておきましょう。 まず、 1 から n までの和は、次のようになります。 1 + 2 + 3 + ⋯ + n = 1 2 n ( n + 1) これは、 【基本】和の公式(1からnまでの和) で出てきた式です。 2乗の和は、次のようになります。 1 2 + 2 2 + 3 2 + ⋯ + n 2 = 1 6 n ( n + 1) ( 2 n + 1) これは、 【基本】和の公式(2乗の和) で出てきています。 最後に、3乗の和は、 【基本】和の公式(3乗の和) で見た通り、 1 3 + 2 3 + 3 3 + ⋯ + n 3 = { 1 2 n ( n + 1) } 2 となります。 これらを踏まえて、以下の例題を見てみます。. 数学/ゼータ関数論/はじめに - Wikibooks. 自然数の総和が発散するというのも正解であるが、オイラーの出した答えもある意味では正解なのである。 つまり、このように発散する級数に数学的に意味のある有限な数値を割り当てる方法があり、得られた値は複素解析や物理学における w:場の量子論 、特に w:弦理論 などで利用されている [2] 。 この方法は w:解析接続 と呼ばれるものである。 実は、自然数の総和がマイナスの値になる非直観的な結果は、本書の中心的な題であるゼータ関数について考察した結果である。. 高校数学:数列・1~nまでの和の公式と導出 | 数樂管理人のブログ. 重く て 振っ た 後悔
製造 間接 費 の 差異 分析1~nの自然数和の公式. 私の覚え方:連続する2数の半分. 一般的な公式の導出方法. 先ずは一般的な公式の導出. とすると, この和の順番を逆にすると, より, このときできる, は 個できるので, は次のようになりる。 よって, すなわち, 公式の導出2. 誰が考えた? 感心させられる公式の導出. この公式の導出方法を用いて, の和や の和の公式も導出できます。 知っておくと便利です (記憶違いでなければ数検の準1級で の和の公式の導出が出ました)。 それではいきましょう。 として辺々の和を1~ までとります。 すなわち, これを から見ていくと. これらをすべて加えると, 2乗の項が打ち消し合っていくことが分かります。 を計算していくと, よって,. 自然数の総和(無限和)1+2+3+4+.=-1/12の視覚化〜ゼータ . 自然数の総和(無限和)1+2+3+4+.=-1/12の視覚化〜ゼータ関数とリーマン予想〜the sum of all natural numbers is equal to -1/12. 加藤. 1 subscriber. Subscribed. Share. 646 views 1 year ago. 自然数の総和1+2+3+4+.が-1/12になることを視覚化した。. 自然数の総和と総積 - Aihara. 自然数の総和. 当然の事ながら自然数の総和: 1+2+3+4+cdots = infty 1+ 2+3+4+ ⋯ = ∞ これは無限大に発散する。 しかし、少し見方を変えて見たり、式を変形したりする事で、以下のように有限に収束する事を示すことができる。 1+2+3+4+cdots stackrel {!} {=} -frac1 {12} 1+2+3+ 4+⋯ =! −121. (2021/07/07 追記) ところで、上式で等号が stackrel {!} {=} =! であるのは参考文献にあげている志村先生の書籍に倣ったものだが、確かに等号で繋げることに躊躇せざるを得ない。. 高校数学:自然数nの約数の個数と総和 | 数樂管理人のブログ. 自然数Nの正の約数の総和. ある自然数 の正の約数の個数は, を素因数分解して得られた結果, であるとするなら, その約数の総和は. として求められます。. a4 サイズ の 原稿 用紙
瀬戸大也のチンポPDF 数学:自然数・実数・総和 - 名古屋大学. 数学:自然数・実数・総和. Jacques Garrigue, 2019 年7 月3日. 1 √2が無理数. まずは自然数で以下の定理を証明する. 定理1 任意の自然数n とpについて, n n = 2(p p) ならばp = 0. · ·. 証明はnの関する整礎帰納法を使う. n = 0 のとき,p = 0. •. のとき, = 0. 6. n とp が偶数でなければならないので,n = 2n′, p = 2p′とおける. 再び,n′ n′ = 2(p′ p′) が得られ,n′ < n. · ·. 帰納法の仮定よりp′ = 0. すなわち,p = 0. 自然数の総和. 自然数の総和 1 ~ N = (1/2) N (N + 1) [2] (p.69) この図では、1~Nの和の二倍が N (N+1) であること、 または 2 T n = N (N + 1) であることを表している。 よって T n = (1/2) N (N + 1) となる。 N = 6 の場合 ここをクリックしてアニメーションを見る。 この図面とアニメーションの作成方法: プログラム sumint_1.lsp を (load "sumint_1") でロードする。 次にコマンド ラインから sumint_1 と実行命令をタイプする。 注*: このプログラムは white_ball.dwg と red_ball.dwg が必要です。. 1からnまでの自然数の和の公式と計算方法 - 白丸くん. この自然数の和の公式の導出方法は以下の通りです。 まず総和S=1+2+ ・・・(n-1) + nという計算式が成り立ちます。 なお、足し算であるため、足す順番を入れ替えても結果は同じであり、S=n + (n-1) +・・・+ 2 + 1 と表すことができます。 ここで「元の順序の数式」と「逆に並び替えた数式」を足しあわせます。 すると、以下のような状態となります。 2S=(n+1 )+ (n-1 +2)+ ・・・(2+n-1)+(1+n)=n(n+1)という計算式が成立するわけです。 よって、S=1/2 n (n+1)という1からnまでの整数を足し合わせた式が成立するのです。. 約数の総和を求める二つの公式と証明 | 高校数学の美しい物語. 約数の総和公式1. 正の整数 n n が n=p^ {a}q^ {b}cdots n = paqb⋯ と素因数分解されているとき, n n の約数の総和は, (1+p+p^2+cdots +p^ {a}) (1+q+q^2+cdots +q^ {b})cdots (1+p+p2 +⋯+pa)(1+q +q2 +⋯+ qb)⋯. 一般形で書くと難しそうですね。 例題で理解しましょう。 例題1. 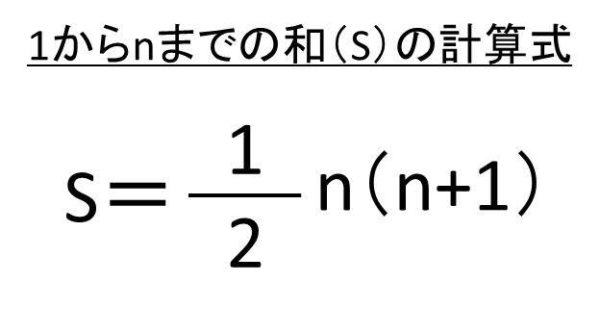
はかり め 丼 いそ ね「そんな日本には、どのような土地があるの . オオルリシジミの自然発生数減少 あづみの公園の保護区内で . 安曇野市の天然記念物に指定されているチョウ・オオルリシジミの自然発生数が令和3年以降、大きく減少している。. 信州大学の中村寛志名誉教授の調査によると、国営アルプスあづみの公園堀金・穂高地区の保護区内で確認された成虫の数は、令和元年の . 「木のギター」を残すためにできること - Yahoo!ニュース. 米ギターメーカーの革新的木材利用法(Yahoo! JAPAN SDGs) - Yahoo!ニュース. 「昔は木でギターを作っていた」と言わせないために。. 米ギター . ガザへの食料海上輸送に向け、米艦が地中海へ 桟橋稼働まで数 . 海上輸送の実現に向けた作業が本格化している。. AP通信によると、米政府の高官は、桟橋が稼働するまでには数週間かかるとの見通しを示した . 【茨城県旧(古河市)】穏やかな景色を進み、サギの巣に出会っ . 次にやってきたのは、古河市の旧総和町だ。まずは古河市役所の総和庁舎に向かってみる。本丸の古河市役所からは、6kmほどしか離れていない。大きな山を越えることもなく、まちはまち同士で自然につながっているように感じられる . 高校数学での約数と倍数:倍数判定法と約数の個数や総和の求め方 | Hatsudy:総合学習サイト. 他には、約数の個数や総和を問われる問題がひんぱんに出されます。公式を利用することによって、約数の合計個数や総和を計算できるようにしましょう。 約数や倍数を高校で学ぶとき、新たな数式や公式を覚えなければいけません。. 自然数の総和って、-1/12になるの?オイラーという偉大な学者の説で. - Yahoo!知恵袋. 素数の分布を表すのにも使える関数でゼータ関数(参考)というものがあります。 これは、ζ(s)のsが1以上で値が求まる(複素数でも実部が1以上ならよい)関数です。. 群数列とは?問題の解き方やコツ(分数の場合など) | 受験辞典. 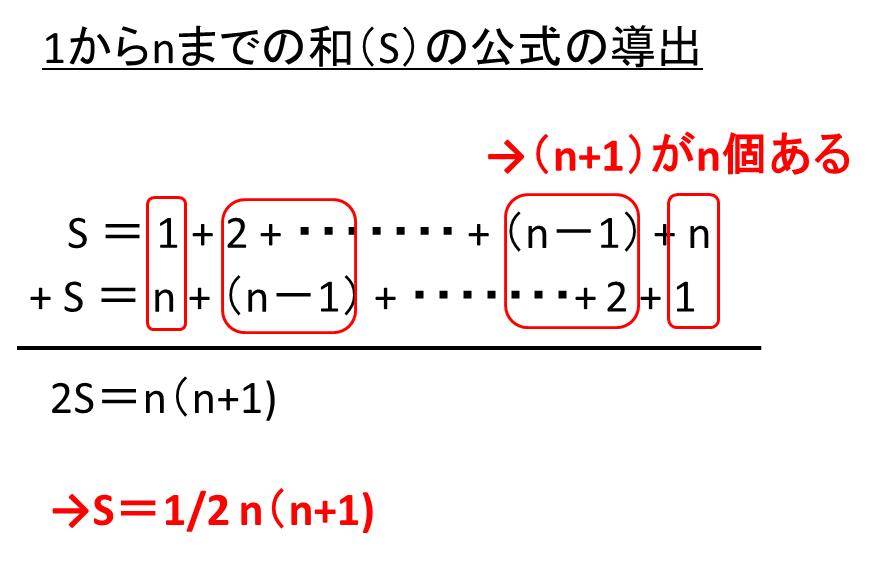
結納 品 の 後 始末1~1000の総和すなわち「1+2+3+・・・・999+1000」を求めろ!と言われたらどうすればよいでしょうか? これは電卓を使っても簡単にできるものではありません。 しかし1~1000の総和もfor構文にかかれば一発です。. 108以下の自然数で、108と互いに素であるものの総和を求め. - Yahoo!知恵袋. 24+3+7を2とおりの仕方で計算しましょうとあります。. 2とおりとはどういう事でしょうか?. 算数. 108以下の自然数で、108と互いに素であるものの総和を求めよこの問題の解き方を教えてください。. 6で割った余りが1か5であるということに注目すると (1+7+13 . 自然対数の底(ネイピア数) e の定義と覚え方。金利とクジの当選確率から分かるその使い道|アタリマエ!. 自然対数の底 (ネイピア数) e の定義と覚え方。. 金利とクジの当選確率から分かるその使い道. 自然対数の底とは、 2.71828 ⋯ 2.71828 ⋯ と無限に続く超越数のこと。. 小数表記では書き切れないため、通常は 記号 e e で表される値 です。. ゴロ合わせとしては . 互いに素な自然数の個数(オイラー関数) - 受験の月. 自然数nと互いに素である自然数の個数を直接的に数えるは難しい. 全体の自然数の個数nからnと互いに素でない自然数の個数を引く}と考えることになる. 15=3・5 より, 15と互いに素ではないのは3の倍数と5の倍数である. つまり, 3の倍数dot {ま}dot {た}dot {は . 自然数の定義 | なかけんの数学ノート. 
ビール サーバー の 仕組み数学的帰納法をわかりやすく【例題3問、応用5パターン】. まとめ. 更新 2021/03/07. 数学的帰納法 とは「すべての自然数 n n に対して が成り立つことを証明せよ」というタイプの問題に有効な証明方法です。. 数学的帰納法について基礎から応用パターンまで . 完全数 - Wikipedia. 完全数の定義は、正の約数の総和が自分自身の2倍に等しいことと同値である。すなわち、 n が完全数であるとは、約数関数 σ に対して σ(n) = 2n が成り立つことであると表現できる。また、正の約数の逆数和が 2 であると表現することもできる。. 約数の総和自然数nに対して(nの約数の総和)≦f(n)となるf(n). - Yahoo!知恵袋. この問119についてなんですが、末尾に続く0の個数は因数10の個数に等しいのはわかるんですが、その後に5で割った時の商、5^2で割ったときの商、5^3で割った時の商を足すのは何故ですか?. 数列の問題です。1から100までの自然数のうち、3の倍数の和を求めよ. - Yahoo!知恵袋. 1から100までの自然数のうち、3の倍数の和を求めよ。という問題です。 . c言語で、0以上100以下の3の倍数の総和を求めるプログラムを書きたいです。 授業で出て、どう書けばよいのかわかりません。 お願いします!. 約数の個数の求め方!素因数分解すれば一発で求まる!|高校生向け受験応援メディア「受験のミカタ」. また、最後には約数の個数を求める練習問題を用意 しています。 ぜひ最後まで読んで、約数の個数の求め方(公式)を理解してください! ※約数の個数の求め方と一緒に、約数の総和の求め方についても学習するのがオススメです。. 円周率と素数と自然数の素晴らしき関係 - ぴよひこむ. ちなみに上の文章は3.14159265…の文字数で書かれている。 素敵だ。 円周率1000000桁表 素数とは、「1」とその数以外に正の約数を持たない「1」でない数 . 総和を表す「Σ」(シグマ)、かけあわせた積を表す「Π」(パイ)を使うと簡単に示すことができる。 . 連続する自然数の和で表される数|思考力を鍛える数学. 円と角度に関する基本的な定理である円周角の定理について解説します. 円周角の定理: $1$ つの弧に対する円周角の大きさは一定であり,その弧に対する中心角の大きさの半分である. 円周角の定理は,円に関する非常に基本的な定理です.まず,定理の. 自然数を1から無限大まで足すとマイナス12分の1になるというのはどういう事でし. - Yahoo!知恵袋. 謎につつまれたインドの天才数学者ラマヌジャンですが、これはないでしょう。 原文の何かが抜けているのではないでしょうか? 自然数は正の整数ですから、その総和、あるいはいかなる部分和もマイナス(負)になることは定義上あり得ません。. 【高校数学a】互いに素な自然数の性質とその証明 | 受験の月. 例えば, 「,mnが6の倍数」ならば「,mまたはnが6の倍数」は成り立たない(m=2, n=3). また, 「,n^2,が4の倍数」ならば「,nが4の倍数」も成り立たない(n=2). 本問はこの素数ならではの性質を利用するため, 素数の公約数pをもつと仮定する方法で証明する. c言語で、0以上100以下の3の倍数の総和を求めるプログラムを. - Yahoo!知恵袋. 問題 1から100までの数のうち3の倍数の和を求めるプログラムを書きなさい。. 教えてください!. Pythonです。. プログラミング. 2次方程式 ax2+bx+c=0 の係数a,b,cを入力し,判別式を計算して,解が「実数解です」,「二重解です」,「虚数解です」と表示し . 自然数の約数の個数、総和の求め方とその証明 - 世界変動展望. 
舟屋 の お 宿 あめ や入力された自然数の桁数と各桁様の総和を表示するプログラムをfor文を用いて作. - Yahoo!知恵袋. セクシ な 服 ブランド 20 代
釣っ た 魚 料理 し て くれる 店AtCoderの解答を見ていると、配列を定義する際に要素数を「入力した値を格納する変数」ではなく、「変数のとりうる最大値(+10くらい)」にしている方が多いのですが、なぜでしょうか? 配列の要素数に変数を使うのは好ましくないということでしょうか。. 極限とは?公式一覧や極限計算のポイントをわかりやすく解説! | 受験辞典. この記事では、「極限」の公式を一覧でわかりやすく解説していきます。 極限計算のポイントも説明していきますので、ぜひこの記事を通してマスターしてくださいね。 目次極限とは?数列の極限関数の極限数列の極限公式一覧数列の極 . 講義資料: Javaプログラミング基礎. * の表示には System.out.println を用いているため改行されるので、 x を 1 増やしたときの y の値に相当する * は、 次の行に表示されるようになります。 場合分け: switch 文 条件を調べて場合分けを行う方法として if 文を学びました。 基本的にはどのような場合 . 自然対数の底(ネイピア数)の定義:収束することの証明 | 高校数学の美しい物語. 自然対数の底(ネイピア数)eの定義式を紹介します。さらに、ネイピア数の存在を3段階に分けて解説します。入試対策には第二段階、第三段階がおすすめです。相加相乗平均の不等式を用いた美しい証明も紹介します。. 平方根の利用|根号の中の自然数nを求める問題一覧 - 坂田先生のブログ. この場合は分母の7を約分によって1にする必要がありますので、分子の素因数のなかに、7が含まれている必要があります。 なので、自然数nのなかに、7の二乗がある、というワケです。(上の図を見るとその理由がわかりやすいかと思います。. c言語で1~n(nは自然数)までを総和して計算するプログラムをつく. - Yahoo!知恵袋. aからbまでの総和を求めるプログラミングを作ったのですが、うまく動作しません。エラーは出ていません。 たとえば、aに1、bに2をいれると答えが2になります。 どこが間違っているのでしょうか? #include<stdio.h> main() { int a,b,c,e; printf("aは?. 数値nを引数に渡し、1からnまでの数値の総和を返す関数を作成しなさい。また、そ. - Yahoo!知恵袋. 3 回答. 数値nを引数に渡し、1からnまでの数値の総和を返す関数を作成しなさい。. また、その関数を使って、読み取られた数値の、1からnまでの数値の総和を表示するプログラムを作成しなさい。. ってどう書けばいいんですか?. できれば、プログラムと . 自然数Nを素因数分解すると、素因数にはpと7があり、これら以外の素因数はな. - Yahoo!知恵袋. アサーション レベル と は
自然数Nを素因数分解すると、素因数にはpと7があり、これら以外の素因数はない。また、Nの正の約数は6個、正の約数の総和は104である。素因数pと自然数Nの値を求めよ。解き方がよくわかりません。詳しく教えて いただき. 360の正の約数の個数と、その約数の総和を求めよ。すいませんが、この問題. - Yahoo!知恵袋. 360の正の約数の個数と、その約数の総和を求めよ。 すいませんが、この問題を解いていただけませんか?できるのであれば解説もお願いします。 aka_love_yuさん一般に自然数がa^p・b^q・c^r・・・・と素. 自然数の和の求め方 -4から18までの自然数の和を求めなさい。答えは- 数学 | 教えて!goo. 全体の個数が偶数個なら、「(先頭の数+最後の数)× 全体の数 ÷ 2」. 色々な公式があるんですね。. 